In 1993, the U.S. Geological Survey, in cooperation with the Washington State Department of Transportation, began a study to update these flood frequency estimates, incorporating data collected through the 1992 water year, and to develop regional regression equations by which flood discharges could be estimated at ungaged sites. However, because some very large floods occurred after 1992, the USGS, in cooperation with the Washington State Department of Transportation and the Washington State Department of Ecology, expanded that study to include all data collected through the 1996 water year. Flood peaks that occurred during a prolonged and intense storm in February 1996 exceeded previous historic peak discharges recorded at several gaging stations in Washington.
The preferred method of expression of flood frequency is the annual exceedance probability. The annual exceedance probability is the probability that a flood of a certain magnitude will occur or be exceeded in any 1-year period. Thus, a flood discharge with an exceedance probability of 0.02, or 2 percent, has a one-in-fifty chance of being equalled or exceeded each year. Another method of expressing flood frequency is as a recurrence interval---the average time interval in years between consecutive occurrences of an annual peak discharge equal to or greater than a certain magnitude. The recurrence interval corresponding to the annual peak discharge for a certain exceedance probability flood is given by the reciprocal of the exceedance probability. Thus, a flood with an exceedance probability of 0.02 has a recurrence interval of 50 years.
The flood-frequency analyses used annual maximum instantaneous discharge data collected through the 1996 water year, which are stored in the USGS National Water Information System (NWIS) database. The results of the flood-frequency analyses were used in conjunction with data stored in the NWIS basin-characteristics file to develop regression equations for estimating flood frequencies at ungaged sites. The State was divided into nine regions for the regression analyses on the basis of hydrologic unit code boundaries.
Local and regional variations in precipitation are influenced primarily by the Olympic Mountains and the Cascade Range. In western Washington, mean annual precipitation ranges from less than 20 inches in the rain shadow of the Olympic Mountains to more than 220 inches along the crest of the Olympic Mountains (U.S. Department of Commerce, 1965). Precipitation along the crest of the Cascade Range exceeds 140 inches in some places. In eastern Washington, mean annual precipitation ranges from less than 10 inches in parts of the Columbia River Basin to about 40 inches near the southeastern and northeastern corners of the State.
In eastern Washington, floods generally occur in the foothills of the Cascade Range and in the highlands of northeastern Washington during spring snowmelt. In some areas of eastern Washington, flooding may occur during the winter when rain or unseasonably warm weather melts accumulations of snow. Flooding may also occur in small basins in response to summer thunderstorms.
The stations given in table 1 and all other tables containing gaging-station data are listed in downstream order by USGS gaging station numbers. The first two digits (12, 13, or 14) designate major basin subdivisions of the State. Stations with numbers beginning with 12 are located on streams tributary to the Pacific Ocean or the Columbia River upstream from the mouth of the Snake River; stations with numbers beginning with 13 are located on streams tributary to the Snake River; and stations with numbers beginning with 14 are on streams tributary to the Columbia River below the mouth of the Snake River.
Estimates of flood discharge and frequency were computed for all 527 gaging stations using an interactive version of USGS computer program J407 (Kirby, 1981), which implements guidelines established by the U.S. Water Resources Council (1981). The U.S. Water Resources Council suggests that separate flood-frequency curves be computed for each type of flood from a mixed population of floods (U.S. Water Resources Council, 1981), but the detailed study required to segregate peak flows by cause was beyond the scope of this project; therefore, no attempt was made to analyze any of the annual flood series separately for mixed populations. Statistical procedures were used to identify high and low outliers in systematic station records. High outliers known or believed to be the highest during an extended period of time were treated as historic flood peaks. Flood peaks identified as low outliers were deleted and then a conditional probability adjustment was applied to all the remaining peaks to determine the flood frequency estimates. In a few cases, visual inspection of the frequency curves identified small peaks that departed from the fitted relation (a sharp downward break in the curve), but were not identified as low outliers by the statistical procedures. A user-defined low-discharge threshold was used to omit such peaks from the flood-frequency analysis.
Not all of the available peak-flow data could be used in the flood-frequency analyses. Stations for which more than 25 percent of the peak-flow record consisted of zero flows were not included in the analyses (U.S. Water Resources Council, 1981, p. 5-1). Also, if part of the systematic record for a station included periods of regulated flow, those periods were not included in the analysis. In some cases, part of the systematic record for a station was excluded from the frequency analysis because only gage heights (and not discharge) were recorded for some years. Flood-frequency results were not included for stations at which the peak discharge data appeared to be representative of and significantly influenced by mixed populations of floods and for which it appeared that no single flood-frequency curve would adequately fit the peak discharge data.
In this study, a log-Pearson Type III distribution was fit to
the data for each station using the method of moments as described by the
U.S. Water Resources Council (1981). The base 10 logarithms of the mean,
standard deviation, and skew coefficient were used to compute the logarithm
of the discharge, 
, at
a selected exceedance probability using the following equation:
, (1)
= mean of the logarithms
of peak flows,
= factor that is a function
of the logarithm of the skew coefficient and the selected exceedance probability,
and
= standard deviation of the
logarithms of peak flows.
were obtained
from the table in appendix 3 of the U.S. Water Resources Council guidelines
(1981). For this study, the skew coefficient used to obtain 
in the above equation was estimated by weighting the station skew coefficient
and a generalized skew coefficient in inverse proportion to their individual
mean-square errors. The generalized skews and their mean-square errors
used for this study were those determined by the U.S. Water Resources Council
(1981). A detailed study of the regional (generalized) skews for the State
of Washington was not done for this study.
Flood-frequency estimates were determined graphically for a small number of gaging-station records because the log-Pearson Type III distribution did not accurately fit the peak discharge data.
Flood discharges computed for exceedance probabilities of 0.5, 0.1, 0.04, 0.02, and 0.01 are given in table 2 (first line of data for each station), along with the 95-percent confidence interval for each computed flood magnitude (second line of data). This interval is the range that, with a probability of 95 percent, contains the true flood magnitude for a particular exceedance probability. Confidence intervals were not determined for flood-frequency estimates determined by graphical techniques.
A review of previous flood-frequency studies for Washington indicated that various combinations of nine identified physical and climatic basin characteristics should be sufficient to produce equations by which flood magnitudes and frequencies can be accurately estimated. Brief descriptions of the nine identified basin characteristics are as follows:
,
in square miles, upstream from the gaging station; determined by planimetering
the contributing drainage area on a topographic map;
,
in feet per mile; determined by extending the main stream channel upstream
to
, in
miles, from the gage to the basin divide; measured along the channel from
the gage to the basin divide;
---the
mean basin elevation, in feet above sea level; determined by finding the
average elevation of at least 20 equally spaced points in the drainage
basin as indicated by a transparent grid overlay;
---the percentage
of the contributing drainage area made up of lakes, ponds, and swamps;
determined by placing a transparent grid over the drainage-basin map and
counting the number of squares occupied by water or swamp surfaces; to
prevent computing the logarithm of zero, storage values of zero percent
were changed to 0.01 percent before running regression analyses;
---the
percentage of the contributing drainage area covered by forests; estimates
of forest cover were obtained from the Washington State Department of Natural
Resources; forest cover may also be determined by the grid-sampling method
on a suitable large-scale map; to prevent computing the logarithm of zero,
forest cover values of zero percent were changed to 0.01 percent before
running regression analyses;
---mean
annual precipitation, in inches, determined by locating the basin on the
precipitation map (plate 1 and U.S. Weather Bureau, 1965), placing a transparent
grid over the map, and averaging the values determined at each grid intersection;
---the
24-hour rainfall, in inches, that can be expected on the average of once
every 2 years within the basin, obtained by using the grid-sampling
method from precipitation-frequency maps for the State of Washington (Miller
and others, 1973); and
---the
mean minimum January air temperature, in degrees Fahrenheit; determined
by using the grid-sampling method on an equal-temperature map from the
U.S. Department of Commerce (1965).Flood-frequency determinations for all of the gaging stations and their associated basin characteristics were placed in a single data set for an initial regression analysis to attempt to determine the geographic regions within the State for which separate regression equations should be developed. The residuals (the differences between the flood magnitudes obtained from the flood-frequency analyses and the flood magnitudes obtained from the regression equations) were plotted on a statewide map. Using this same procedure, Cummans and others (1975) were able to subdivide the State into 12 regions, each with its own set of regression coefficients and constants. However, no meaningful grouping of the residuals computed during this study could be made. Adjacent basins and, in some cases, parts of the same basin were located in different regions when residuals were used as the grouping criteria. Therefore, hydrologic-unit code boundaries were used instead to group the stations into separate geographic regions believed to have different hydrologic characteristics. The State of Washington is divided into eight hydrologic units, each composed of several cataloging units (U.S. Geological Survey, 1976). Each cataloging unit, in turn, contains one to several major stream basins. For this study, an additional region was created by dividing the Columbia River Basin hydrologic unit into two subunits: one encompassing the Columbia Plateau (Region 7) and the other encompassing mostly those areas east of the Cascade Range and north or west of the Columbia River (Region 4). The nine geographic regions are shown on figure 1, and the distribution of gaging stations used for the regression analysis in each region is shown on figures 2-10.
Regression analyses for each region included the use of the ordinary least-squares technique to obtain a preliminary list of which basin characteristics were most influential in affecting peak flows at the 5 percent level of significance. All nine of the basin characteristics identified in previous reports as being the most important in determining flood discharges were considered for inclusion in each regional regression equation. In addition, a subjective decision was made in cases where two or more basin characteristics were about of equal significance in estimating flood magnitude. In these cases, the relative ease by which values for the basin characteristics could be obtained was considered in the selection of which characteristics to use in the development of the regression equations for estimating flood magnitudes and frequencies for ungaged streams. The objective in making such decisions was to greatly simplify the application of an equation with only a minor decrease in its accuracy. Consequently, a regression equation may contain a basin characteristic that is slightly less significant than another characteristic that was considered but not included in the equation or it may contain fewer basin characteristics than the "best" regression equation defined by the regression analysis.
The physical and climatic basin characteristics determined most significant in predicting flood discharge were contributing drainage area and mean annual precipitation for regions 1, 2, 3, 4, 6, and 9; and contributing drainage area only for regions 5, 7, and 8. All basin characteristic values were computed in accordance with both the NWIS basin-characteristics file guidelines and the National Handbook of Recommended Methods for Water-Data Acquisition (U. S. Department of the Interior, 1977). The basin characteristic values for the stations used in the regression analyses are given in table 3.
Main channel slope, one of the basin characteristics found to be statistically significant in the development of the regression equation for region 5, was removed from the final regression equation because it had a negative regression coefficient, which doesn't seem physically realistic. It is believed that its statistical significance in the regression analysis may be the result of either a spurious relationship or the fact that it may be a surrogate for one or more other basin characteristics.
Once it was determined which basin characteristics should be used for each regression region, then the flood-frequency data for each region were analyzed using the generalized least-squares technique (Tasker and Stedinger, 1989) to determine equations for estimating flood magnitude and frequency for ungaged sites within the regions. This method differs from the ordinary least-squares method by weighting each station used in an analysis on the basis of the number of years of peak flows in the station record and by the distance between stations. Ordinary least squares were not used to develop the regression equations because two assumptions that are made in the use of that method---that the residuals of the data have equal variances and that each residual is independent of all others---are usually violated to some degree in hydrologic regression analysis. In the case of peak-flow data, both of these assumptions are often violated. Peak-flow records are usually of differing lengths, and nearby basins may be affected by the same weather patterns, leading to unwanted correlations in the peak flows.
The mathematical model used to define the relation between flood discharge and basin characteristics for each region was
, (2)
= flood discharge, in cubic
feet per second,
= basin characteristics,
= regression constant, and
= regression coefficients.
, 
)
to base 10 logarithms:
. (3) The regression equations developed for the nine flood-frequency
regression regions are presented in table 4. The standard error of prediction
(given in table 4) is a measure of how well the regression equation predicts 
from the data used in the analysis; a higher degree of uncertainty is associated
with a higher standard error. The highest percent standard error of prediction
is found in Region 8 (133 percent for an exceedance probability of 0.5).
Although the exact source of this high value is not known, it is probably
a combination of the time sampling error and model error. The time sampling
error is the error due to using a peak flow record that might not represent
the entire range of peak flows possible at a site. The model error is the
error due to not having the most influential variable in the regression
equation. Although the time sampling error may be reduced by accumulating
more years of peak-flow data, a reduction in model error is limited by
the availability of basin-characteristic data and the cost and effort involved
in collecting other types of basin data. Also, including more explanatory
variables in the regression equation may reduce the model error at the
cost of ease of use and data availability for the user. The equivalent
years of record (given in table 4) is also a measure of the predictive
ability of the regression equation, expressed as the number of years of
actual peak-flow data required to achieve results equal to those obtained
from the regression equation.
Weighted estimates of flood magnitude for the 504 gaging stations used in the regression analyses (table 2) were obtained using the weighting procedures presented in appendix 8 of the guidelines of the U.S. Water Resources Council (1981), in which two different estimates of flood magnitude (from the frequency analysis and from the regression equation) are weighted inversely proportional to their variance. The weighted estimates generally provide better estimates of the true flood discharges than those determined from either the flood-frequency analysis or the regression analysis alone.
. (4)
, (5)
= flood discharge, in cubic
feet per second, at the ungaged site,
= weighted flood discharge,
in cubic feet per second, at the gaged site (from table 2),
= contributing drainage
area, in square miles, at the ungaged site,
= contributing drainage
area, in square miles, at the gaged site, and
= exponent for each region
as follows.
for each
region was determined by regressing the discharges for each exceedance
probability on the drainage areas for the stations in the region. The drainage
area exponents determined from the regression analyses for each of the
exceedance probabilities were averaged to produce the single exponent for
each region.
Equation 5 should only be used if the basins of the gaged and ungaged sites have similar basin characteristics. Therefore, if a large tributary enters the stream between the gaged and ungaged sites, and the tributary basin has much different topography, vegetation, or other basin characteristics that could affect flood discharges, then the appropriate regression equation from this report should be used to estimate flood-frequency discharges for the ungaged site.
The following is an example of the determination of the flood
discharge with an exceedance probability of 0.01 at an ungaged site on
the Naselle River (Region 1). The contributing drainage area at the ungaged
site (
) is 47 square miles.
The contributing drainage area at the gage (
)
on the Naselle River (station number 12010000 in table 2) is 54.8 square
miles.
The drainage area of the ungaged site 
,
expressed as a percentage of the drainage area of the gaged site 
,
is given by:
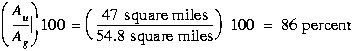, The weighted discharge, 
(obtained from table 2, third line for station 12010000) is 12,100 cubic
feet per second. The exponent, 
,
for Region 1 is 0.92. The computed discharge, 
,
is
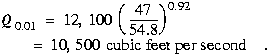
A further limitation on the use of the regression equations is that they should not be used for basins in which urbanization has taken place. Because the regression equations were developed using data from unurbanized basins, application of the equations to urbanized basins could produce misleading results. Techniques for estimating flood discharges on urban streams are presented by Sauer and others (1983).
The results of the frequency analysis were combined with physical and climatic basin characteristics values to develop equations that can be used to compute peak discharges for ungaged streams. The State was divided into nine regions, based on hydrologic unit boundaries, and a separate set of equations was developed for each region. Basin characteristics shown to be important in estimating flood discharge include contributing drainage area and mean annual precipitation.
Bailey, E.G., 1960, Floods in the Nooksack River Basin, in Water resources of the Nooksack River Basin and certain adjacent streams: State of Washington, Department of Conservation, Division of Water Resources Water-Supply Bulletin No. 12, p. 95-98.
Bodhaine, G.L. and Robinson, W.H., 1952, Floods in Western Washington, Frequency and magnitude in relation to drainage basin characteristics: Geological Survey Circular 191, 124 p.
Bodhaine, G.L. and Thomas, D.M., 1960, Floods in Washington, magnitude and frequency: U.S. Geological Survey Open-File Report, 25 p.
---------1964, Magnitude and frequency of floods in the United States, part 12, Pacific Slope Basins in Washington and upper Columbia River Basin: Geological Survey Water-Supply Paper 1687, 335 p.
Cummans, J.E., Collings, M.R., and Nassar, E.G., 1975, Magnitude and frequency of floods in Washington: U.S. Geological Survey Open-File Report 74-336, 46 p.
Drost, B.W. and Lombard, R.E., 1978, Water in the Skagit River Basin, Washington: State of Washington, Department of Ecology Water-Supply Bulletin 47, 247 p.
Fenneman, N.M., 1931, Physiography of western United States: New York, McGraw-Hill Book Company, Inc., 534 p.
Haushild, W.L., 1979, Estimation of floods of various frequencies for the small ephemeral streams in eastern Washington: U.S. Geological Survey Water- Resources Investigations Open-File Report 79-81, 22 p.
Kirby, William, 1981, Annual flood frequency analysis using U.S. Water Resources Council guidelines (Program J407), chapter I, section C of WATSTORE user's guide: U.S. Geological Survey Open-File Report 76-435, v. 4, p. C-1 to C-57.
Miller, J.F., Frederick, A.H., and Tracey, R.J., 1973, Precipitation atlas of the western United States, vol. IX, Washington: National Oceanic and Atmospheric Administration NOAA Atlas 2, 43 p.
Nassar, E.G. and Walters, K.L., 1975, Water in the Palouse River Basin, Washington: State of Washington, Department of Ecology Water-Supply Bulletin 39, 246 p.
Rantz, S.E. and Riggs, H.C., 1949, Magnitude and frequency of floods in the Columbia River Basin, in U.S. Geological Survey, 1949, Floods of May-June 1948 in Columbia River basin: Geological Survey Water-Supply Paper 1080, p. 317-469.
Richardson, Donald, 1965, Effect of logging on runoff in upper Green River basin, Washington, a progress report: U.S. Geological Survey Open-File Report, 45 p.
Sauer, V.B., Thomas, W.O., Jr., Stricker, V.A., and Wilson, K.V., 1983, Flood characteristics of urban watersheds in the United States: U.S. Geological Survey Water-Supply Paper 2207, 63 p.
Tasker, G.D., and Stedinger, J.R., 1989, An operational GLS model for hydrologic regression: Journal of Hydrology, v. III, nos. 1-4, p. 361-275.
Thomas, B.E., Hjalmarson, H.W., and Waltemeyer, S.D., 1994, Methods for estimating magnitude and frequency of floods in the southwestern United States: U.S. Geological Survey Open-File Report 93-419, 211 p.
Thomas, C.A., Broom, H.C., and Cummans, J.E., 1963, Magnitude and frequency of floods in the United States, part 13, Snake River basin: Geological Survey Water-Supply Paper 1688, 250 p.
U.S. Department of Commerce, 1965, Climates of the states---Climate of Washington, in Climatography of the United States, no. 60-45: U.S. Weather Bureau, 27 p.
U.S. Department of the Interior, 1977, National handbook of recommended methods for water-data acquisition: U.S. Geological Survey Office of Water Data Coordination, variously paged.
U.S. Geological Survey, 1976, Hydrologic unit map--1974, State of Washington: Reston, Va, U.S. Geological Survey, 1 sheet, scale 1:500,000.
U.S. Water Resources Council, 1981, Guidelines for determining flood flow frequency: U.S. Water Resources Council Bulletin 17B, 28 p., 14 appendixes.
U.S. Weather Bureau, 1965, State of Washington, mean annual precipitation, 1930-1957: Portland, Oreg., Soil Conservation Service, map M-4430, 1 sheet, [no scale].
Walters, K.L., 1974, Water in the Okanogan River Basin, Washington: State of Washington, Department of Ecology Water-Supply Bulletin 34, 136 p.
Walters, K.L. and Nassar, E.G., 1974, Water in the Methow River Basin, Washington: State of Washington, Department of Ecology Water-Supply Bulletin 38, 73 p.
Williams, J.R., and Pearson, H.E., 1985a, Streamflow statistics and drainage-basin characteristics for the southwestern and eastern regions, Washington, Volume I, Southwestern Washington: U.S. Geological Survey Open-File Report 84-145-A, 424 p.
---------1985b, Streamflow statistics and drainage-basin characteristics for the southwestern and eastern regions, Washington, Volume II, Eastern Washington: U.S. Geological Survey Open-File Report 84-145-B, 662 p.
Williams, J.R., Pearson, H.E., and Wilson, J.D., 1985a, Streamflow statistics and drainage-basin characteristics for the Puget Sound region, Washington, Volume I, Western and southern Puget Sound: U.S. Geological Survey Open-File Report 84-144-A, 330 p.
---------1985b, Streamflow statistics and drainage-basin characteristics for the Puget Sound region, Washington, Volume II, Eastern Puget Sound from Seattle to the Canadian border: U.S. Geological Survey Open-File Report 84-144-B, 420 p.
For additional technical information from the principal author, send email to Steve Sumioka (ssumioka@usgs.gov) or call him at (253) 428-3600 x2645.
This on-line report is adapted from Magnitude
and Frequency of Floods in Washington, 1998, by S.S. Sumioka, D.L. Kresch,
and K.D. Kasnick, which is published as U.S. Geological Survey Water-Resources
Investigations Report 97-4277. Copies of the report may be purchased from
the USGS Information Services, Box 25286,
Denver, Colorado 80225, telephone 888-ASK-USGS (888-275-8747).
USGS--Water Resources
of Washington State
USGS--Water Resources of the United
States
U.S. Geological Survey
This page is http://
wa.water.usgs.gov
/pubs/wrir/flood_freq/index.html
Last modified: Tue Jun 16 15:25:12 1998
Converted to the Web by James Lyles (jrlyles@usgs.gov).
This page is maintained by John M. Clemens (jclemens@usgs.gov).
